Objectifs - Interface
La problématique
Le domaine de recherche de Christophe Cudennec est la modélisation hydrologique à base géomorphologique pour la gestion territoriale de l'eau. Ce titre scientifique décrit la recherche de modèles pluie-débit qui permettent de quantifier certaines relations entre le territoire et les circulations d'eau, et donc d'envisager un aménagement du territoire en vue de la réduction des dégâts dus aux fortes pluies.
Lorsque l'on parle ici de modèle, il s'agit d'une simplification de la réalité pour pouvoir appliquer des concepts et faire de la quantification. Un modèle pluie-débit permet de lier les pluies qui couvrent un territoire avec la quantité d'eau s'écoulant à un endroit donné pour un temps donné. Une fois un tel modèle correctement défini, l'opération inverse peut être envisagée, c'est-à-dire déduire de la quantité d'eau qui s'écoule les caractéristiques de la pluie tombée.
La problématique qui se cache derrière cette recherche est et sera de plus en plus d'actualité dans la région du Languedoc-Roussillon : les crues et la gestion de l'aménagement territorial afin de faire face à ces crues. Ce sont les précipitations de fortes intensités plutôt que le total annuel des précipitations qui causent souvent les catastrophes naturelles, comme les inondations exceptionnelles. Les précipitations fortes dépassent la capacité d'infiltration du sol et se traduisent par un ruissellement de surface qui peut devenir excessif et générer des crues importantes en aval.

Figure A.1.1 - - Le rôle intégrateur du bassin versant à l'échelle de l'évènement hydrométéorologique (Source Cudennec, 2001)
Le problème actuel est que chaque aménagement, aussi bien à l'échelle de l'agriculteur qui cherche à protéger ses récoltes qu'à l'échelle de la commune qui cherche à protéger ses habitants et leurs biens, résout des problèmes locaux de crues. Les acteurs individuels aménagent leur partie de territoire de manière à réduire les conséquences localement, sans forcément étudier l'effet de ces aménagements sur les territoires plus en aval. Pour prévenir au mieux les conséquences de ces évènements naturels, l'idée est d'étudier le comportement du territoire et de ces aménagements à un plus haut niveau d'organisation des cours d'eau et donc de résoudre les problèmes à ce niveau d'organisation : celui du bassin versant.
Le bassin versant est un territoire sur lequel les gouttes de pluie qui tombent s'écoulent, puis se rejoignent en un même endroit : l'exutoire (remarque : il existe toujours une partie de la pluie qui est stockée dans des réserves souterraines ou en surface, qui retourne à l'atmosphère par évaporation ou qui " fuit " en profondeur). Un bassin versant possède des frontières naturelles qui suivent des lignes naturelles et définissent généralement une zone fermée. Nous pouvons donc définir qu'un bassin versant est une zone délimitée par un contour. Les gouttes de pluie peuvent aussi s'infiltrer dans la roche et former des réservoirs ou des nappes souterraines ; il existe alors une circulation souterraine des eaux.
Dans un bassin versant, l'eau s'écoule toujours d'un point haut vers un point bas, soit de l'amont vers l'aval. Sur son chemin, elle recueille les eaux d'autres cours d'eau, plus petits. Ils sont appelés les affluents.
Il faut noter l'existence, à la surface du bassin versant, d'un système longitudinal, le réseau de drainage ou réseau hydrographique, défini comme l'ensemble des cours d'eau naturels ou artificiels, permanents ou temporaires, qui participent à l'écoulement. Ce réseau est plus ou moins développé selon différents facteurs (géologie, climat, pente du terrain, etc.). La carte 1 présente l'exemple du réseau hydrographique du bassin versant de Skhira :
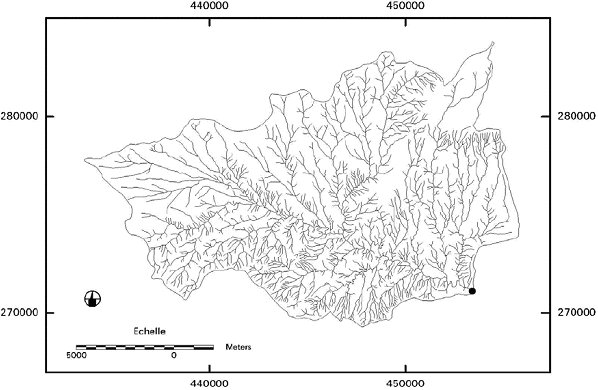
Figure A.1.2 - - Présentation du bassin versant de Skhira (Source Cudennec et al, 2005)
En définitive, le réseau hydrographique est donc un objet ramifié et hiérarchisé. Pour un bassin versant, outre l'exutoire, unique extrémité aval, le réseau hydrographique est composé de points particuliers : les extrémités amont, appelées sources, ainsi que les jonctions entre plusieurs - en général deux - branches du réseau, c'est à dire les confluences. La fraction du réseau hydrographique comprise entre deux confluences ou bien entre une confluence et une extrémité est appelée bief.
Etudes de bassins versants - Caracteristiques du reseau hydrographique" />
Dans notre objectif, la plupart des statistiques géomorphométriques d'un bassin versant seront générées à partir des caractéristiques du réseau hydrographique. Nous les définissons donc maintenant afin de ne pas perdre le lecteur par des définitions hydrologiques au milieu de la description du logiciel.
Donc, la caractéristique la plus simple à calculer, mais dont tous les autres calculs dépendent, est la longueur de chacun des biefs du réseau. En connaissant ces longueurs, il sera possible de calculer les longueurs pour d'autres éléments du bassin versant.
Une des principales études à faire sur un bassin versant est celle de la classification de son réseau hydrographique. La classification est facilitée par un système de numérotation des biefs. L'ordre des cours d'eau est donc une classification qui reflète la ramification du cours d'eau. Il existe plusieurs types de classification des biefs, dont la classification de Strahler (1952), qui est la plus utilisée. C'est celle que nous utiliserons.
Cette classification permet de décrire sans ambiguïté le développement du réseau de drainage d'un bassin de l'amont vers l'aval. Nous allons tout d'abord considérer l'ordre de Strahler sur un réseau hydrographique binaire car, dans un milieu naturel, les confluences multiples sont rares. Donc, sur un réseau hydrographique binaire, l'ordre de Strahler se base sur les règles suivantes :
- Tout bief issu d'une source est d'ordre 1
- Tout bief formé par la confluence de deux biefs d'ordre i et j respectivement prend l'ordre :
- i+1 si i = j
- Max (i,j) sinon
La figure suivante illustre l'ordre de Strahler sur le réseau hydrographique binaire du petit bassin versant tunisien de Hadada.
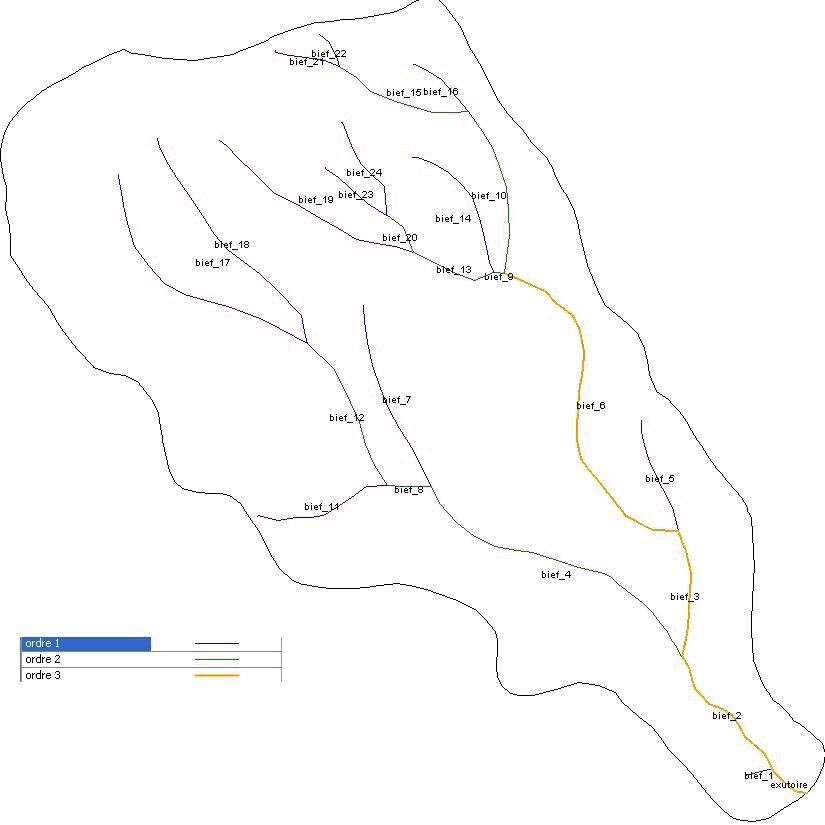
Figure A.1.3 - Application des ordres de Strahler au réseau hydrographique binaire du bassin versant de Hadada (Tunisie)
Mais le traitement des MNT (Modèles numériques de terrain) peut engendrer des réseaux hydrographiques non binaires. Il faut donc adapter l'ordre de Strahler à des réseaux non binaires. Donc, voici le calcul de l'ordre de Strahler généralisé sur un réseau quelconque (binaire ou non) :
- Tout bief issu d'une source est d'ordre 1
- Tout bief formé par la confluence de n biefs d'ordres a, b, c, …, n prend l'ordre :
- max + 1 si au moins deux biefs sont d'ordre max = Max(a, b, c, … , n)
- max sinon avec max = Max(a, b, c, … , n)
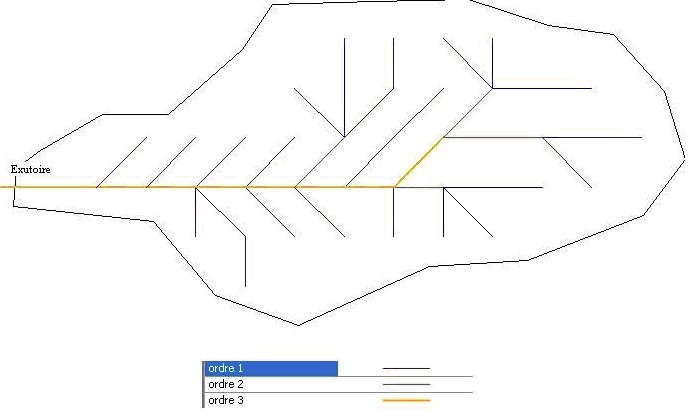
Figure A.1.4 - Application des ordres de Strahler à un réseau hydrographique non binaire extrait d'un MNT
- RL = Li+1 / Li, où Li est la longueur moyenne des tronçons d'ordre i.
- RC = Ni / Ni+1, où Ni est le nombre de tronçons d'ordre i.
- La composante hydraulique d'ordre 1 composée du bief_18
- La composante hydraulique d'ordre 2 composée des biefs biefs_12, bief__8 et bief_4
- La composante hydraulique d'ordre 3 composée des biefs biefs_2 et exutoire.
Enfin, les longueurs des chemins (de chaque bief et de chaque point de la grille d'échantillonnage) et de leurs composantes sont considérées en termes statistiques et cartographiques.
L'analyse du comportement hydrologique d'un bassin versant (système hydrologique) s'effectue par le biais de l'étude de la réaction hydrologique du bassin face à une sollicitation (la précipitation). Cette réaction est mesurée à l'exutoire du système hydrologique par l'observation d'un hydrogramme qui n'est autre que la représentation de l'évolution du débit Q en fonction du temps t.
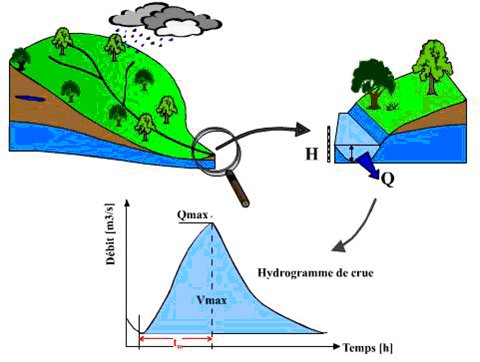
Figure A.1.4 - Principes d'analyse du comportement hydrologique du bassin versant et hydrogramme résultant (Source http://hydram.epfl.ch/e-drologie/)
Il s'agit donc d'analyser le débit d'eau dans le cours du temps à l'exutoire d'après des relevés spatio-temporels de la pluie.
Pour calculer ce débit au cours du temps, il suffit alors d'appliquer un champ de pluie, c'est-à-dire la quantité de pluie tombée à un instant t et à une position dans l'espace p, à la représentation du bassin versant sous forme de zones isochrones. On peut alors prévoir, à chaque pas de temps suivant, la quantité d'eau provenant de ce champ de pluie et arrivant à l'exutoire. Il faut pour cela calculer la pluie nette, c'est-à-dire la quantité de pluie qui va s'écouler à travers le réseau hydrographique, à partir de la pluie brute, c'est-à-dire la quantité d'eau spécifiée par le champ de pluie. Il suffit alors d'appliquer le champ de pluie dans le temps et dans l'espace, c'est-à-dire de prendre en compte la variabilité de l'intensité et de l'emplacement des nuages de pluies, et on obtient un débit théorique dans le temps que l'on peut comparer au débit réel.
Pour cela, il est donc envisageable de déduire les zones isochrones en terme de temps d'écoulement, à partir de caractéristiques du réseau hydrographique. Les zones isochrones définies représenteront alors les zones d'égal temps de parcours de l'eau jusqu'à l'exutoire via le réseau hydrographique. Le tracé du réseau des isochrones permet donc de comprendre en partie le comportement hydrologique d'un bassin versant et l'importance relative de chacun de ses sous bassins.
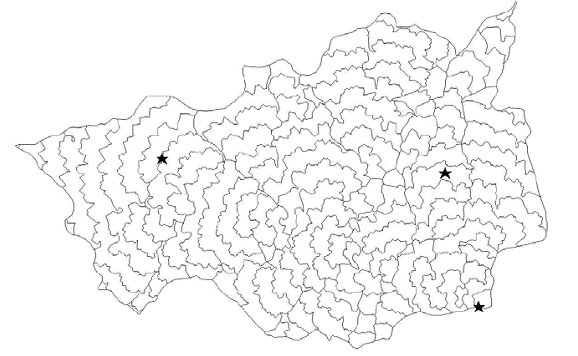
Figure A.1.5 - Présentation des isochrones du bassin versant de Skhira (Source Cudennec et al, 2005)
Les zones isochrones et les comportements hydrauliques alors définis, on aboutit alors au graphique qui suit :
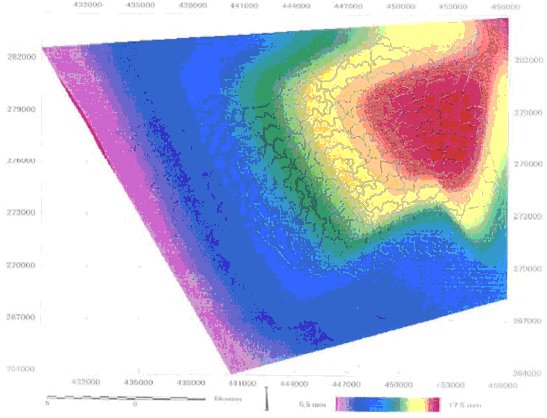
Figure A.1.6 - Champ de pluie appliqué aux zones isochrones d'un bassin versant (Source Cudennec et al, 2005)
Généralités
Les données sources du protocole proviennent de relevés topographiques, de l'interprétation de photographies aériennes ou de lecture de cartes topographiques. Il s'agit donc d'images vectorielles qui représentent le contour et le réseau hydrographique de bassins versants dont les coordonnées sont exprimées dans le même système de projection.
Le protocole définit certaines contraintes telles que :
- Le contour du bassin versant doit être un polygone
- L'ensemble des arcs de l'image du réseau hydrographique doit être connexe, ramifié et binaire.
Entre autres, le protocole permet d'observer les caractéristiques de n'importe quel point de la zone drainée par rapport à cette topologie. Pour cartographier ces caractéristiques sur le territoire du ou des bassins versants étudiés, il suffit donc d'étudier l'ensemble des points d'un échantillonnage du plan. C. Cudennec propose pour cela de s'appuyer sur une grille régulière dont chaque intersection est un point d'échantillonnage. La mise en forme numérique des informations acquises aboutit alors à des images raster dont les pixels sont centrés sur les points de la grille.
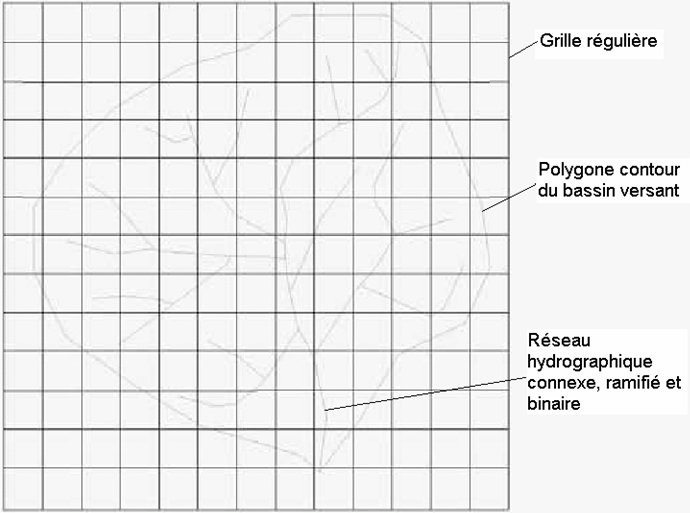
Figure A.2.1 - Application d'une grille régulière sur un bassin versant (Cudennec, 2000)
L'idée est de considérer le réseau hydrographique comme un arbre binaire. En effet, le réseau hydrographique est un objet ramifié fortement hiérarchisé où les confluences multiples sont suffisamment rares pour être négligées et assimilées à un ensemble de confluences simples. Le réseau hydrographique est donc organisé selon les deux règles suivantes :
- Le bief exutoire est l'unique extrémité aval et a deux biefs affluents à l'amont.
- Tout autre bief a un unique bief aval et éventuellement deux biefs affluents à l'amont ; en l'absence d'affluent, le bief a pour extrémité amont une source.
Une fois décrits comme une arborescence, certains attributs du réseau sont alors calculables. Nous citerons l'ordre de Strahler, des statistiques de dénombrement et des mesures de longueur sur les biefs et les tronçons.
Une grille régulière pour étudier le bassin versant
La grille est définie par la coordonnée haut-gauche du début de la grille, un pas et une distance maximale de couverture dans le sens des abscisses, un pas et une distance maximale de couverture dans le sens des ordonnées. Les points ainsi définis constituent le centre de chaque maille de largeur et de hauteur définis par les pas de la grille. La grille couvre le bassin versant dans son ensemble.
Certains calculs sont définis pour chaque point de la grille qui appartient au bassin versant tel que : l'ensemble des arcs constituants le chemin hydraulique (et ses composantes hydrauliques), la longueur hydraulique (la longueur jusqu'à l'exutoire), la longueur séparant le point de la grille du réseau, l'appartenance au bassin versant, … (cf. schéma ci dessous)
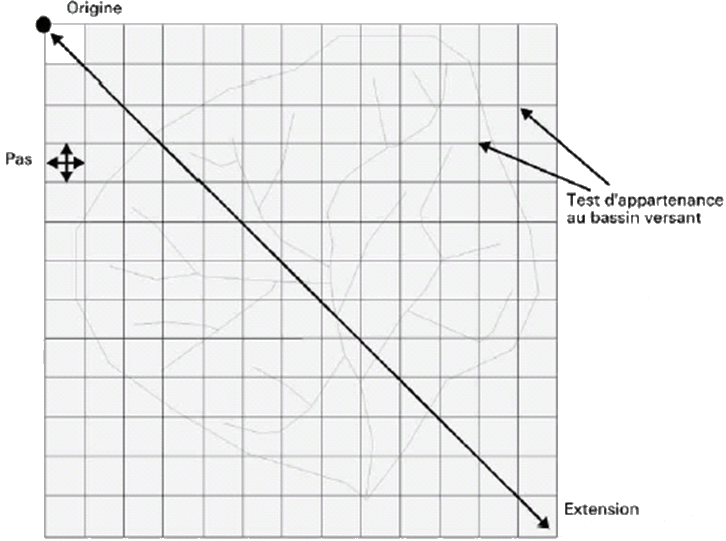
Figure A.2.3 - Schéma d'application d'une grille d'échantillonnage (Cudennec, 2000)






